ecuaciones con numeros racionales
Un
método para resolver ecuaciones racionales es reescribir las
expresiones racionales en términos de un denominador común. Entonces,
como sabemos que los numeradores son iguales, podemos resolver la
variable. Para ilustrar esto, veamos una ecuación muy simple:
x = 3
Como el denominador de cada expresión es el mismo, los numeradores deben ser equivalentes también. Esto significa que x = 3.
Esto es también válido para ecuaciones racionales con polinomios:
2x – 5 = 11
x = 8
Una
vez más, como los denominadores son los mismos, sabemos que los
numeradores deben ser también iguales. Por lo que podemos igualarlos el
uno con el otro y resolver x.
Debemos comprobar nuestra solución en la expresión racional original:
La solución funciona, y como x = 8 no resulta en una división entre 0, la solución es válida.
Cuando
los términos en una ecuación racional tienen denominadores distintos,
resolver la ecuación necesitará trabajo extra. Aquí hay un ejemplo:
|
Ejemplo
|
|
Problema
|
Resolver la ecuación 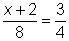
|
|
|
|
|
|
|
No hay valores excluidos porque ambos denominadores son constantes
|
|
|
|
|
Encontrar el común denominador y reescribir cada expresión con ese denominador
El común denominador es 8
|
|
|
x + 2 = 6
x = 4
|
|
Como los denominadores son el mismo, los numeradores deben ser iguales para que la ecuación sea válida, Resolver x.
|
|
|
|
|
Comprobar la solución sustituyendo x por 4 en la ecuación original
|
|
Solución
|
x = 4
|
|
|
|
|
|
|
|
Otra
forma de resolver ecuaciones racionales consiste en multiplicar ambos
lados de la ecuación por un común denominador. Esto elimina los
denominadores y convierte la ecuación racional en una ecuación de
polinomios. Aquí está el mismo ejemplo que acabamos de resolver:
|
Ejemplo
|
|
Problema
|
Resolver la ecuación
|
|
|
|
|
|
|
No hay valores excluidos porque ambos denominadores son constantes
|
|
|
|
|
Multiplicar ambos lados por el mínimo común denominador
|
|
|
x + 2 = 6
|
|
Simplificar
|
|
|
x + 2 – 2 = 6 – 2
x = 4
|
|
Resolver x
|
|
Solución
|
x = 4
|
|
|
|
|
|
|
|
Ahora
que entendemos las técnicas, veamos un ejemplo que tiene variables en
el denominador. Recuerda que cuando hay variables en el denominador,
necesitamos encontrar los valores que están excluidos del dominio porque harían el denominador cero.
Para resolver la ecuación, podemos multiplicar ambos lados por el mínimo común denominador:
|
Ejemplo
|
|
Problema
|
Resolver 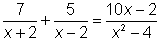
|
|
|
|
|
x + 2 = 0
x = -2
x – 2 = 0
x = 2
(x + 2)(x – 2) = 0
x = -2, 2
|
|
Primero determinar los valores excluidos. Estos son los valores de x que harían 0 el denominador
|
|
|
denominadores:
x + 2
x – 2
x2 – 4 = (x – 2)(x + 2)
mínimo común denominador:
(x – 2)(x + 2)
|
|
Encontrar el común denominador de x – 2, x + 2, y x2 – 4
Como (x – 2) y (x + 2) son factores de x2 – 4, el mínimo común denominador es (x – 2)(x + 2) o x2 – 4
|
|
|
|
Multiplicar ambos lados de la ecuación por el común denominador
|
|
|
7x – 14 + 5x + 10 =10x – 2
12x – 4 =10x – 2
|
|
Simplificar
|
|
|
12x – 10x – 4 = 10x – 10x – 2
2x – 4 = -2
2x – 4 + 4 = -2 + 4
2x = 2
x = 1
|
|
Resolver x
Asegurarse que la solución no es un valor excluido. (No lo es)
|
|
|
|
|
Comprobar la solución en la ecuación original
|
|
Solución
|
x = 1
|
|
|
Resolver la ecuación 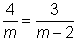 , m , m 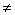 0 o 2 0 o 2
A) m = 2
B) no existe solución
C) m = 8
|
Hemos
visto que hay más de una forma de resolver ecuaciones racionales.
Porque ambas técnicas manipulan y reescriben los términos, algunas veces
pueden producir soluciones que no funcionan en la forma original de la
ecuación. Este tipo de respuestas se llaman soluciones extrañas.
Estas soluciones son artefactos del proceso de solución y no son
respuestas reales. Es por eso que siempre debemos comprobar las
soluciones con las ecuaciones originales — podríamos encontrar que se
obtienen declaraciones inválidas o producen expresiones indefinidas.
|
Resolver la ecuación:
A) x = -1
B) x = -1, 6
C) x = -4, 3
D) no existe solución
|
Resolvemos
ecuaciones racionales encontrando un común denominador. Podemos
entonces seguir cualquiera de dos métodos. Podemos reescribir la
ecuación de tal manera que todos los términos tengan el común
denominador y podemos resolver la variable con sólo los numeradores. O
podemos multiplicar ambos lados de la ecuación por el denominador común
para que todos los términos se vuelvan polinomios en lugar de
expresiones racionales.
Un
paso importante cuando resolvemos ecuaciones racionales es rechazar
cualquier solución extraña de la respuesta final. Las soluciones
extrañas son soluciones que no satisfacen la forma original de la
ecuación porque producen declaraciones inválidas o son valores excluidos
que hacen que el denominador sea igual a 0.


 Es la porción de espacio limitada por dos semiplanos que se llaman caras.
Es la porción de espacio limitada por dos semiplanos que se llaman caras.


































